Petri-Netze

Petri-Netze wurden 1962 von C. A. Petri auf Basis der Graphentheorie entwickelt. Sie eignen sich zur Modellierung, Analyse und Simulation von dynamischen Systemen mit nebenläufigen und nichtdeterministischen Vorgängen, z.B. in Betriebssystemen oder Echtzeitsystemen, aber auch Organisationsabläufen wie in Büros oder Herstellungsverfahren.

Elemente des Petri-Netzes
Das dynamische Verhalten
Hierarchiebildung
Datenstrukturierung
Eignungsschwerpunkte

Elemente des Petri-Netzes

Ein Petri-Netz ist ein gerichteter Graph, der aus Kanten und zwei verschiedenen Arten von Knoten, den Stellen und Transitionen besteht.

Symbol	Benennung	Bedeutung / Bemerkungen
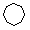	Stelle (Platz)	Zwischenablage für Informationen. Stellen, von denen aus Kanten zu einer Transition T führen heißen Eingabestellen von T. Stellen, zu denen von einer Transition T aus Kanten führen, heißen Ausgabestellen.
	Transition (Hürde)	Verarbeitung von Daten. Anstelle des Rechtecks sind auch Striche gebräuchlich.
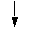	Kante	Die Kanten dürfen jeweils nur von Stellen zu Transitionen oder von Transitionen zu Stellen führen.
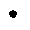	Marke	Kennzeichnung der Belegung einer Stelle.

Elemente eines Petri-Netzes

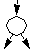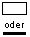
	branch oder Verzweigung
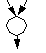	meet, Begegnung oder Wettbewerb
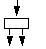	split oder Aufspaltung
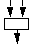	wait, Sammlung oder Rendevouz

Elementare Verknüpfungen

Das dynamische Verhalten

Das Netz kann als Basis für die Darstellung dynamische Vorgänge dienen. Dazu werden die strukturellen Eigenschaften durch Regeln für das dynamische Verhalten ergänzt. Man kann das Netz als Spielbrett betrachten auf dem ein Spiel mit Marken durchgeführt wird. Das Netz beschreibt das grundsätzliche Verhalten eines Systems, das Spiel simuliert einen bestimmten Ablauf.

Das Beispiel in Systemmodell einer Tankstelle als Petri-Netz vermittelt einen ersten Eindruck. Es erfüllt die folgende Aufgabenstellung:

Eine Selbstbedienungstankstelle hat zwei Zafpsäulen. Zu jeder gehört ein Standplatz, so dass ein Auto betankt werden kann, vorausgesetz, die Zapfsäule ist freigegeben. Die Freigabe der Zapfsäule erfolgt durch einen Tankwart, nachdem er nach dem Betanken kassiert hat.

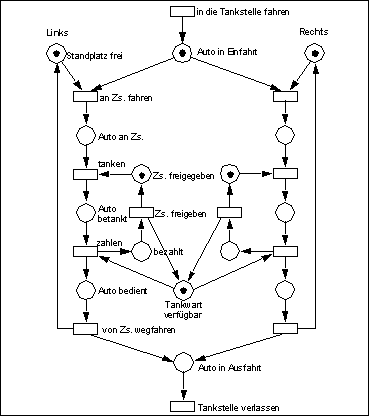
Systemmodell einer Tankstelle als Petri-Netz

Dabei werden bezüglich der Belegung der Stellen mit Marken zwei Spielregeln unterschieden:

strong rule: diese spezielle Regel legt fest, dass jede Stelle mit höchstens einer Marke belegt sein darf (Datentyp boolean). Damit erfüllt eine Stelle eine Bedingung, die entweder erfüllt ist oder nicht. Das entspricht dem Zustandsgraphen der Automatentheorie. Man spricht von einem Bedingungs-Ereignis-System oder bool-Petri-Netz.
soft rule: bei der allgemeinen Regel ist die Belegung einer Stelle mit mehreren Marken zulässig (Datentyp natural). Dabei können für jede Stelle individuell eine obere Grenze festgelegt oder beliebig viele Marken zugelassen werden. Hier spricht man von einem Stellen-Transitions-Netz oder nat-Petri-Netz.

Bei Transitionen muß man zwischen der

Aktivierung (cocession) und dem
Schalten (firing) unterscheiden.

Eine Transition ist aktiviert:

bei der strong rule, wenn alle ihre Eingabestellen markiert und alle ihre Ausgabestellen nicht markiert sind,
bei der soft rule, wenn alle Eingabestellen mit mindestens einer Marke belegt sind und alle Ausgabestellen mindestens noch eine Marke aufnehmen können.

Das Schalten einer Transition kann nur erfolgen, wenn sie aktiviert ist. Aus allen Eingabestellen wird eine Marke entfernt, in alle Ausgabestellen wird eine Marke gesetzt.

Für Beginn und Dauer des Schaltvorganges gibt es keine generellen Regelungen.

Nachfolgend sind in Schaltvorgänge in Petri-Netzen Beispiele für Aktivierung und Schaltvorgang dargestellt.

nicht feuerbereit		aktiviert	Schaltung erfolgt
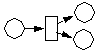	Eingangsbedingung nicht erfüllt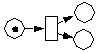
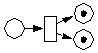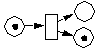	Ausgang noch belegt

Schaltvorgänge in Petri-Netzen

In bestimmten Situationen ergeben sich Konflikte in einem Netzwerk, die jedoch durch Einfügung steuernder Erweiterungen gelöst werden können.

Verzweigungskonflikt		Wettbewerbskonflikt
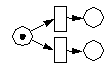	Die Schaltregel gibt keinen Aufschluß darüber, welche Transition schaltet.		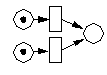Die Transitionen können nicht gleichzeitig schalten, da die Ausgabestelle nur eine Marke aufnehmen kann.
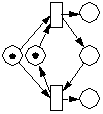	Zusätzliche Schaltbedingung schafft Klarheit. Jetzt wird "getoggelt".		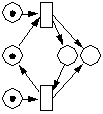Hier geht es jetzt nach dem "Reißverschluss-Verfahren".

Konflikte in Petri-Netzen

Neben den dargestellten Grundtypen gibt es verschiedene Modifikationen. Zum Beispiel werden neben den Datentypen boolean und nat auch allgemeinere Datentypen zugelassen. In der Bürowelt sind die Typen Formular oder Akte gebräuchlich.

Oft werden auch weitere Sorten von Stellen und Transitionen zugelassen, z.B. Stellen zur Beschreibung von Fallunterscheidungen. Das bedeutet eine Änderung der allgemeinen Schaltregel.

Je nach ihre Lage im Netz können Stellen oder Transitionen unterschiedliche Bedeutung haben. In der Bedeutung von Stellen und Transitionen nach Lage im Netz sind alle Möglichkeiten dargestellt und erläutert

Symbole	Bedeutung	Beispiel
	Löschung von Objekten.
	Erzeugung von Objekten.
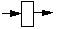	Verarbeitung oder Weitergabe von Objekten.
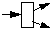	Aufspaltung oder Vervielfachung von Objekten, Beginn einer Nebenläufigkeit.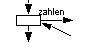
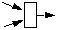	Verschmelzung von Objekten, Synchronisationspunkt, Ende einer Nebenläufigkeit.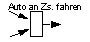
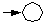	Ablage, z.B. Archiv.
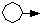	Quelle, Lieferant von Objekten.
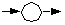	Zwischenablage, Zwischenspeicher.
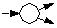	Nichtdeterministische Fortsetzung oder willkürliche Verzweigung eines Prozesses und/oder Beginn einer Nebenläufigkeit.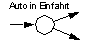
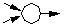	Synchronisationsstelle, gemeinsamer Speicher für Objekte.

Bedeutung von Stellen und Transitionen nach Lage im Netz

Hierarchiebildung

Transitionen und Stellen können in Teilnetze aufgelöst werden, so wie Teilnetze zu Stellen oder Transitionen zusammengefaßt werden können. Dabei ist zu beachten:

Die Schnittstelle des Teilnetzes zum Restnetz bleibt unverändert, d.h. das Teilnetz, das eine Stelle ersetzt hat eine Stelle als Eingang und eine Stelle als Ausgang. Das Teilnetz, das eine Transition ersetzt hat eine Transition als Eingang und eine Transition als Ausgang.

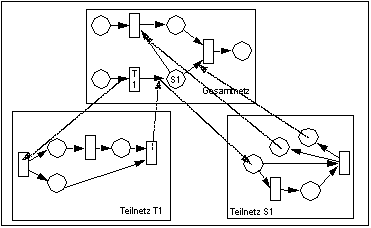
Hierarchien in Petri-Netzen

Noch einige Anmerkungen zum Beispiel Systemmodell einer Tankstelle als Petri-Netz.

Deutlich wird die Parallelität von Prozessen, denn durch die Verdopplung der Betriebsmittels Zapfsäule und Stellplatz ist ein gleichzeitiges Betanken von zwei Fahrzeugen möglich.
Die Stelle Auto in "Einfahrt" ist ein Verzweigungskonflikt, der hoffentlich durch den Fahrer des Autos gelöst wird.
Den Wettbewerbskonflikt an der Stelle Tankwart verfügbar" wird der Tankwart lösen. Kleine Probleme wie fehlendes Wechselgeld sind in dem Modell nicht berücksichtigt, Sie können ja mal darüber nachdenken.
Das Problem der endlosen Autoschlangen vor den Tankstellen, den Warteschlangen", ist in unserem System ebenfalls nicht berücksichtigt. Es ist - wie so häufig - auf die Straße verlagert. Wenn in der Einfahrt der Tankstelle Stauraum für einige Fahrzeuge vorhanden ist, dann sollten wir in unserem Modell nach der soft rule spielen. Die Stelle Auto in Einfahrt" könnte dann z.B. 5 Marken = Autos aufnehmen. Damit hätten wir eine Warteschlange realisiert.

Vorgehen bei der Modellierung

Bei der Modellierung beginnt man zunächst mit einem sehr abstrakten Netz, dem Instanzen-Kanal-Netz. Instanzen entsprechen den Transitionen, sie sind die aktiven Teile des Netzes; in ihnen läuft etwas ab. Die Kanäle, sie entsprechen den Stellen, sind die passiven Teile. Sie leiten etwas weiter oder sie speichern etwas. Das Petri-Netz mit Instanzen und Kanälen zeigt so ein Beispiel.

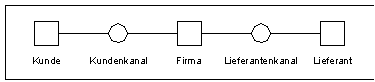
Petri-Netz mit Instanzen und Kanälen

In einem zweiten Schritt werden die Kanäle konkretisiert. Der Kundenkanal kann z.B. aus eingehender Briefpost oder Telefonaten für die Bestellungen und ausgehender Paketpost für die Warenlieferung bestehen.

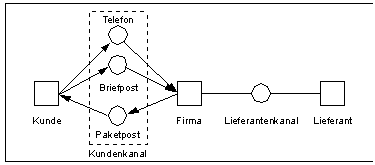
Verfeinerung eines Kanals

Im dritten Schritt werden die Instanzen von außen nach innen verfeinert. Zunächst sucht man nach einer Instanz für jeden dieser verfeinerten Kanäle. Diese neuen Instanzen werden ggf. über neue Kanäle innerhalb der zu verfeinernden Instanz verbunden. Das Beispiel Verfeinerung einer Instanz macht das Vorgehen deutlich.

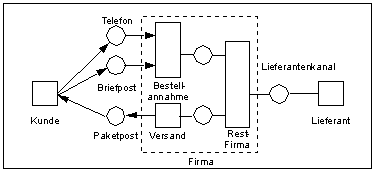
Verfeinerung einer Instanz

Diese Verfeinerungen von Kanälen und Instanzen werden fortgesetzt bis das bestehende oder geplante System vollständig beschrieben ist. Dabei geht das Kanal-Instanzen-Netz in ein Stellen-Tronsitions-Netz oder gar Bedingungs-Ereignis-Netz über.

Datenstrukturierung

In der ursprünglichen Form der Petri-Netze sind keine Sprachelemente zur Spezifikation und Strukturierung von Daten vorgesehen.

Eignungsschwerpunkte

Mit Hilfe von Petri-Netzen läßt sich ein System als Folge von Zuständen und Ereignissen sehr schnell modellieren. Mit dem Markenspiel" kann das Verhalten bzw. das Fehlverhalten des Systems überprüft werden.